TRANSLAÇÃO DE OBJETOS UTILIZANDO MATRIZES

COMPUTAÇÃO GRÁFICA

                Para deslocarmos um ponto do plano cartesiano $($no caso, uma imagem de um ponto gerada por computador devemos usar sua posição$)$, definida pelas suas coordenadas x e y, e realizar a operação de soma de matrizes entre a matriz COORDENADAS DO PONTO P, representada pela matriz $P=\begin{bmatrix}
1 \\ 2
\end{bmatrix}$ e a matriz DESLOCAMENTO (D), representado pela matriz $\begin{bmatrix}
1 \\ 2
\end{bmatrix}$, resultando na matriz final, que traduz as coordenadas do ponto deslocado.

Como exemplo, observe o ponto $P(2,3)$ definido no plano cartesiano: 

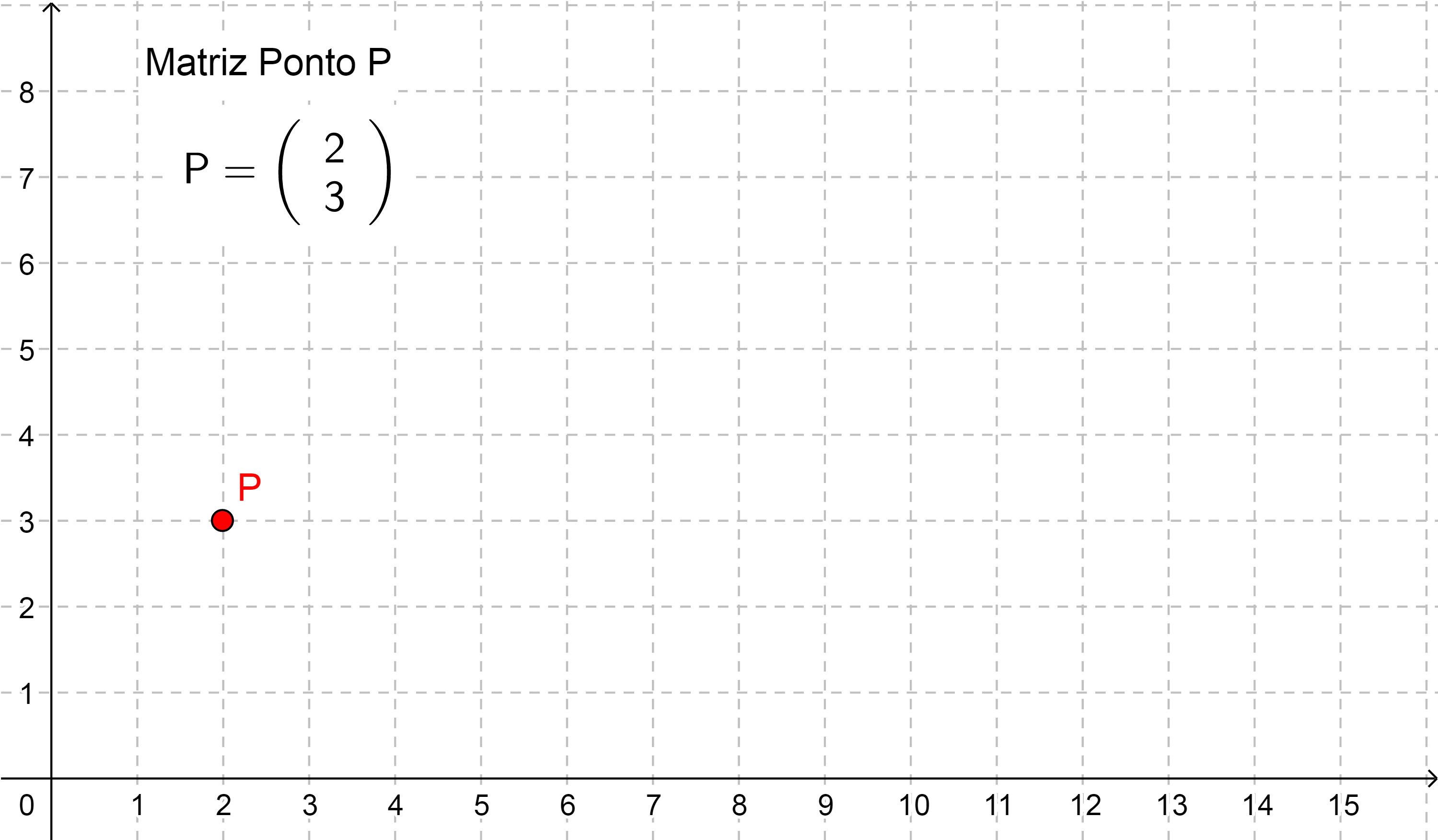
                 Para inserir as coordenadas do ponto $P=(2,3)$ usaremos a matriz $\begin{bmatrix}
x\\ y
\end{bmatrix}$ e vamos inserir o valor da coordenada da abscissa do ponto $P$ no valor $x$ da matriz $($linha 1 e coluna 1$)$ e inserir o valor da coordenada da ordenada do ponto $P$ no valor $y$ da matriz $($ linha 2 e coluna 1).

                    A translação do ponto P $($deslocamento da posição do ponto inicial até a posição final$)$ se dará pela operação de soma entre a matriz P e a matriz com os valores do deslocamento horizontal $($para $x)$ e vertical $($ para $y)$ que queremos para o ponto P.

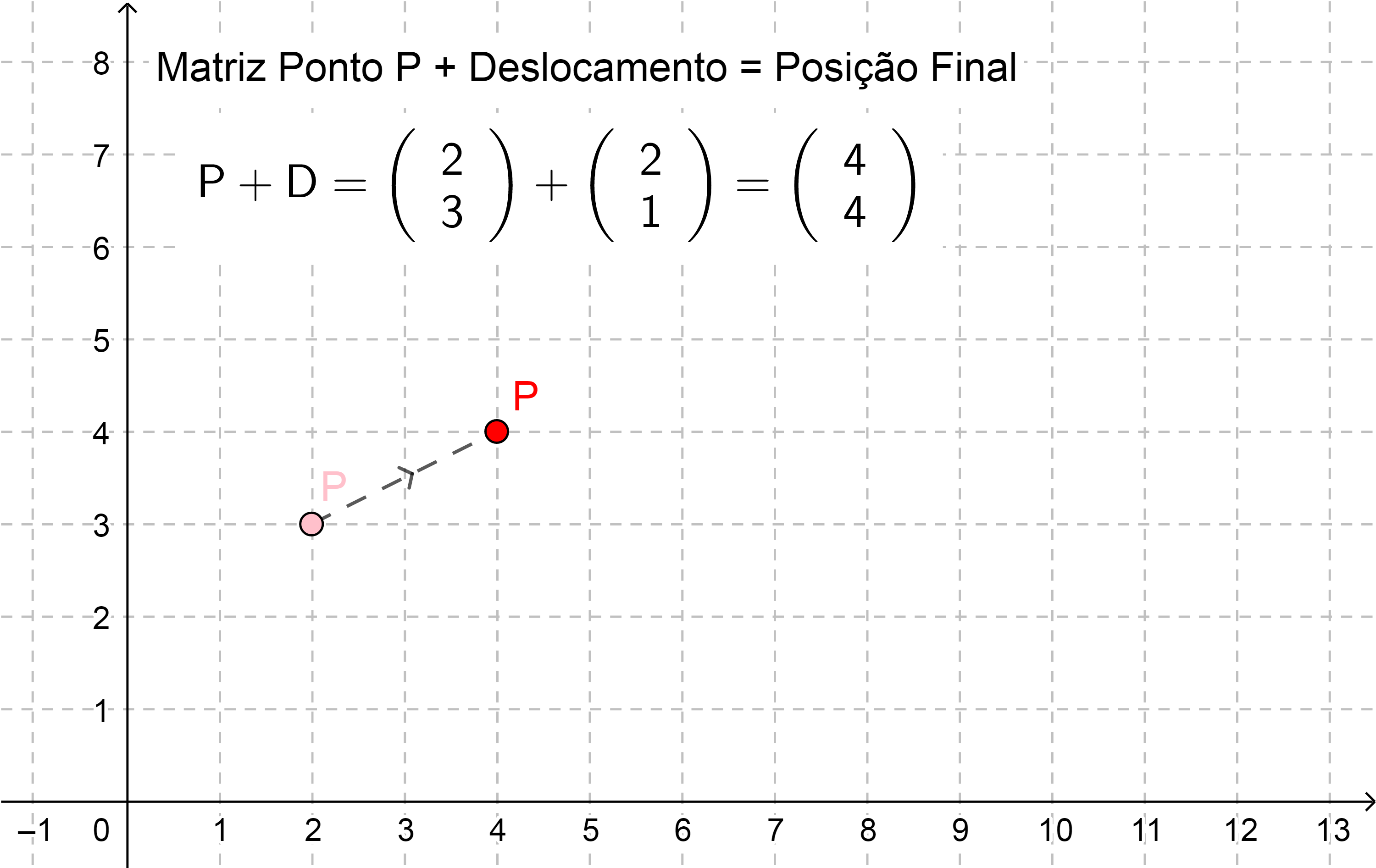
                     Por exemplo, vamos transladar o ponto P em +2 unidades na horizontal $($para a direita$)$ e em +1 unidade na vertical $($para cima$)$. Assim, somando as matrizes $P = \begin{bmatrix}
2\\ 3
\end{bmatrix}$ e $D=\begin{bmatrix}
2\\ 1
\end{bmatrix}$ obtemos a matriz resultante $P + D =\begin{bmatrix}
2\\ 3
\end{bmatrix} + \begin{bmatrix}
2\\ 1
\end{bmatrix} = \begin{bmatrix}
2+2\\ 3+1
\end{bmatrix} = \begin{bmatrix}
4\\ 4
\end{bmatrix}$ que corresponde às coordenadas $(4,4)$ da posição do ponto final do movimento.

Observe o resultado gráfico da operação de soma de matrizes:

• Desloque-o em +4 unidades na horizontal e +2 unidades na vertical;

• Desloque-o em +5 unidades na horizontal e -2 unidades na vertical;

• Desloque-o em -1 unidade na horizontal e +2 unidades na vertical;

• Desloque-o em 2 unidades para a direita e em 3 unidades para cima;

• Desloque-o em 1 unidade para baixo e em 3 unidades para a esquerda;

• Desloque-o em 3 unidades para cima e em 2 unidades para a esquerda;

• Desloque-o em 2 unidades para a direita e em 3 unidades para baixo;

2. O que as coordenadas de deslocamento negativas representam?

3. Qual a diferença entre coordenadas positivas/negativas e os comandos direita/esquerda, cima/baixo?